【トピックス】
精密熱量測定による糖加水分解酵素活性と触媒機構の解析
城所俊一
長岡技科大・生物系
1.はじめに
示差走査熱量計 (DSC) や等温滴定型熱量計 (ITC) などの高精度微小熱量計の装置・解析法の発展により、近年、生体高分子の構造形成や分子間相互作用などの計測に広く用いられるようになってきている1)。通常は、DSCは昇温することで観測される生体分子の立体構造変化を熱的に測定することで、熱変性温度や変性に伴うエンタルピー・エントロピー変化、熱容量変化などを高い精度で評価するのに用いられる。一方、ITCは、生体高分子にリガンドを除々に滴下する際の熱の出入りを観測することで、生体分子とリガンドの結合に伴うエンタルピー変化を評価するとともに、得られる結合曲線から結合定数を求める2)。この際、DSCでは、生体分子のエンタルピーや熱容量の温度依存性、ITCではエンタルピーのリガンド濃度依存性が評価され、“時間”に関する情報は通常表に出ない。このような意味で、現在、生体高分子の測定で用いられている熱測定は「静的」な測定と言える。
酵素機能において最も重要な性質は触媒能である。これは、ある化学反応速度をどれだけ高めることができるかで評価され、化学反応速度を評価することが必要となる。DSCもITCも本来は動的な測定法であり、一定の速度で温度走査をした時 (DSC)、決められた時刻で一定の速度で溶液を滴下した時 (ITC) の単位時間当たりの吸熱/発熱量 (以下では、吸熱速度と呼ぶ) を時間の関数として測定している。通常は、これらの測定値をDSCでは熱容量に変換し、ITCでは時間で積分することで熱量を「静的」に評価している。しかし、現在使用されている高精度のDSCやITCには、10秒程度かそれ以下の装置定数で、1 mLの試料の吸熱速度0.1µWのシグナルを観測することが可能なものがあり、装置定数より長い時間領域で起きる化学反応の「動的」な熱量測定が可能である。(これまで報告されている熱量測定を用いた酵素反応の評価については、最近の解説3)を参照されたい。)
例えば、基質の化学変化に伴うモルエンタルピー変化 (ΔH) が-1 kJ/mol (発熱) とし、1 mMの基質溶液1 mLが1000秒で化学変化をする場合、平均的には1 nmol/s の速度で反応が起き、吸熱速度は-1µWとなる。この程度の熱の出入りがあれば、現在の感度の熱量計で十分に時間経過を追うことが可能である。ちなみに、この時観測される総熱量は1 mJであり、この熱による溶液の温度上昇はわずか0.0002℃程度である。この値をみると、現在の高精度熱量計がいかに微小な熱量を測定しているかが実感できる。
質の化学反応の際の熱を測定することで酵素の触媒能を評価する方法は、様々な利点を持つことが期待される。第一に、基質の化学変化を検出するための特別なプローブを必要としないことが挙げられる。化学反応に伴うエンタルピー変化が熱となり、反応の進行が観測できる。第二に、熱量測定は反応速度を検出するという特徴を持つ。熱量計の観測量である吸熱速度は、反応速度に比例し、基質や産物の量には直接関係しない。したがって基質あるいは産物が非常に多量にある条件でも、微小な化学変化を定量的に計測できる可能性を持つ。第三に、連続的に経時変化を測定するのが容易である。酵素反応について酵素の添加から触媒反応の終了までの全時間領域を高いデータ密度で測定することで、初期基質濃度を変えた測定を行わずにミカエリス定数を高い精度で決定することが可能となる。
本稿では、グルコースがβ-1,4 結合で数個グルコシド結合をしたセロオリゴ糖を基質とし、反転型および保持型のエンドグルカナーゼ (セルラーゼ) の加水分解反応をITCにより観測した最近の我々の研究4)を例として、精密熱量測定による酵素反応測定の実際や糖加水分解反応の基質阻害効果、触媒機構の判別に成功した例を紹介したい。
2.糖加水分解反応の等温滴定熱量測定
酵素による糖の加水分解反応の定量は、適当な分光学的なプローブが存在しない場合が多いため、通常は、溶液中の基質や産物の量を分離・定量したり、加水分解によって新たに生じた還元末端を様々な発色法などを利用して検出・定量することで行われる。このためには、酵素反応を一度停止させてから定量する必要があり、連続的に反応の経時変化を追跡することは困難である。また、短い糖鎖断片を基質にする場合には、還元末端の量の変化が小さいために定量性の高い分析が必要とされる。
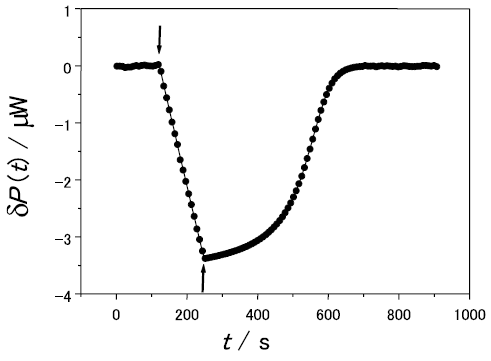
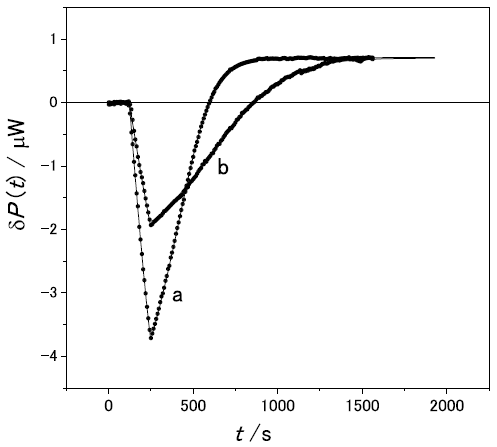
あらかじめ熱量計のセルに1.0 mMのセロヘキサオースを基質として入れておき、これに酵母で組み換え発現・精製した反転型エンドグルカナーゼの溶液をシリンジから滴下して加水分解反応をITCで測定した結果を図1に示す。溶媒はpH4.0, 20 mM酢酸緩衝液、温度は30.0℃で行った。測定中はセルの中は常に一定の速度 (毎分300回転) で回転攪拌を行っている。セルとシリンジに溶液をセットし、温度が一定になった後に攪拌を開始し、攪拌熱 (一定の発熱速度を示す) が安定して観測できるのを確認した後に測定が開始される (図中の時刻0)。図ではこの時の吸熱速度 (単位時間当たりの吸熱量) δP(t)を0としている。測定開始後122秒後 (図中の下向き矢印) から229秒後 (図中の上向き矢印) までの間一定の速度でシリンジから総量60µLの酵素溶液をセルに滴下する。セル中の酵素濃度は、この127秒間をかけて線型に徐々に増加し、最終濃度は0.27µMに達する。セル中の酵素濃度の増加とともに単位時間当たりの発熱量 (発熱速度-δP(t)) がほぼ直線的に増加しているのがわかる。酵素溶液の注入が完了した後、セル中では、一定の酵素濃度の条件で加水分解反応が継続して進行するが、基質が分解されて濃度が除々に減少するにしたがって発熱速度は減少してゆき、ほぼ全ての基質が加水分解されてδP(t)は0に戻る。

この実験条件下では、基質は1カ所でしか加水分解をせず、産物はセロテトラオースとセロビオースであることはHPLCによる分析で別に確認している。すなわち、図1では、基質の中の1カ所のグリコシド結合が加水分解される際の発熱反応を観測していることになる。この場合の酵素反応速度v(t)は、以下のミカエリス・メンテンの式に従うと期待される。

ここで、S(t)は時刻tでの基質の濃度、E0は溶液中の酵素の総濃度であり、kcatとKMはそれぞれ、分子活性 (代謝回転数) とミカエリス定数である。図1の縦軸の値δP(t)は、試料の単位時間当たりの吸熱量であり、定圧条件では、熱力学第一法則より、反応速度v(t)と反応に伴うモルエンタルピー変化ΔH、セル体積Vcを使って、

と表される。特に、最大速度vmaxの時のδP(t)は
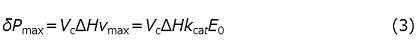
と表される。図1では酵素溶液の滴定修了直後 (上向きの矢印の直後) はほぼ最大速度が観測されているものと考えられる。
定常状態では、反応速度と基質濃度の間には、

の関係があるため、δP(t)を次のように時間で積分することで

と熱量変化δQ(t)を求めると、この値は基質濃度S(t)と

という関係を持つことになる。特に時刻0の時、および基質濃度がミカエリス定数と等しくなった時のδQ(t)を

と表す。ここでS0は基質初濃度である。δQ0は反応に伴う総熱量変化を表し、これを基質初濃度とセル体積の積で除することで、反応に伴うモルエンタルピー変化ΔHを求めることができる。
式 (1) の両辺の逆数をとることで得られる基質濃度の逆数と反応速度の逆数の関係式
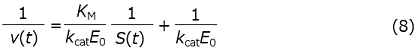
の両辺をVcΔHで除することで、前述の観測量の間に以下の関係式が成立することがわかる。
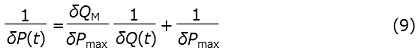
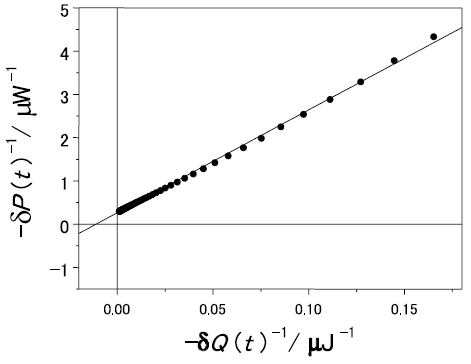
したがって、δQ(t) の逆数に対してδP(t) の逆数をプロットすることで1/S vs 1/v プロット (Lineweaver-Burkプロット) に対応する線型プロットが得られることが期待される。実際、図1の酵素滴定終了後 (上向きの矢印以降) のデータをプロットすると (図2)、データは理論通り直線に乗ることがわかる。直線の傾きと切片から、δPmaxとδQMは、それぞれ、-3.8µW、-91µJと見積もられる。

3.積分型ミカエリス・メンテンの式を利用した反応熱の経時変化の解析
酵素反応の経時変化から酵素活性のパラメーターをより精密に決定するためには、式 (1) に (4) の関係を用い、1回積分して得られる、いわゆる積分型のミカエリス・メンテン式を用いるのが有効である。
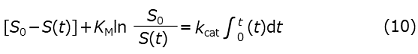
ここでは、図1のように、酵素を滴下し、溶液中の総酵素濃度が増加している時間帯でも適用できるように右辺の酵素濃度を時間の関数として一般化している。ここで、各酵素濃度で定常状態と見なせることを前提としているが、一般には定常状態に影響を与える程度に酵素濃度を変化させるためにはストップドフロー法などの高速混合が必要であり、今回のような酵素濃度の滴下で観測できるのは常に定常状態と考えられる。この時、酵素の滴定終了後の総濃度をE0とし、式 (10) の両辺にVcΔHを乗じて
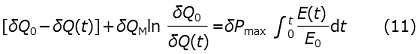
という式を得る。この式は、3つのパラメーター、δPmax、δQM、δQ0と、酵素濃度E (t)を与えられた時、δQ(t)を決める方程式と考えることができる。この方程式は解析的には解けないが、唯一の解が存在することは容易に示すことができ、実際Gauss-Newton法などの数値解法によって迅速に高精度の解を得ることができる。また、同時刻の実験値δP(t)は式 (1) の両辺にVcΔHを乗じることで得られる次式にδQ(t)を代入することで決定される。
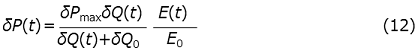
したがって、δP(t)の観測値を元にして、フィッティングパラメーターを非線型最小二乗法を用いて最適化することで先の3つのパラメーターを決定できる。図1のデータからこれらを決めると、δPmax、δQM、δQ0は、それぞれ-3.72µW、-91.9µJ、-1138µJ と決定された。図1の実線が理論値であるが、全ての時間領域で実験値を大変良く説明できる。δPmax、δQMは前の節で線型化プロットから評価した値と一致している。また、δQ0をセル体積 (1.344 mL) と基質濃度 (1.0 mM) の積で除すことでΔHは-0.85 kJ/mol と決まる。これを用いてδPmaxとδQMからkcatとKMを評価すると、それぞれ、12s-1、81µMとなる。このように、定常状態の単純な酵素反応については、等温熱量計を用いてδP(t)を測定・解析することで、反応に伴うモルエンタルピー変化と酵素活性のパラメーターを評価することが可能である。
図1の測定の際に、130秒程度の時間をかけて60µLの酵素溶液を滴下しているが、これは次のような理由のためである。定常状態で酵素反応を測定するための最適な総酵素濃度E0については、通常の酵素反応測定手法と同様、適度な時間範囲で酵素反応が確実に検出できるように設定し、このための必要な酵素をシリンジから滴下することになる。この時、あまり濃い酵素濃度の溶液をシリンジに入れてしまうと、シリンジをセルに挿入して攪拌し熱的に安定するのを待つ間の20分程度の間に、シリンジの先端から漏れだした微量の酵素溶液が有意な速度で酵素反応を進行させてしまう恐れがある。これを抑えるためには、薄い濃度の酵素溶液を使用し、滴下する体積を大きくするのが望ましいことになる。この場合、滴下するスピードが速すぎると、主として混合前の2種類の溶液の温度差に起因するゴースト熱が観測されてしまうことがある。従来法5,6)では、酵素溶液の滴下を終了し、溶液中の総酵素濃度が一定になってからのデータしか解析ができなかったが、本方法では、酵素濃度を時間の関数として理論式に取り込むことで、酵素をゆっくりと滴下した場合でも、滴下している時間帯の酵素反応も含めての全時間領域のデータを用いて解析することができるようになった。
4.オリゴ糖の基質阻害効果
図1の加水分解反応を、基質初濃度を0.5 mMから2.0 mM まで変えて測定し、酵素活性のパラメーターを評価したところ、非常に興味深い結果を得た。すなわち、kcatは基質初濃度に依らずに同一の値を示したが、KMは基質濃度とともに直線的に増加することがわかった。もしも基質あるいは産物が弱い拮抗阻害をする場合には、kcatは一定だが、ミカエリス定数KMappは、基質初濃度S0によって、

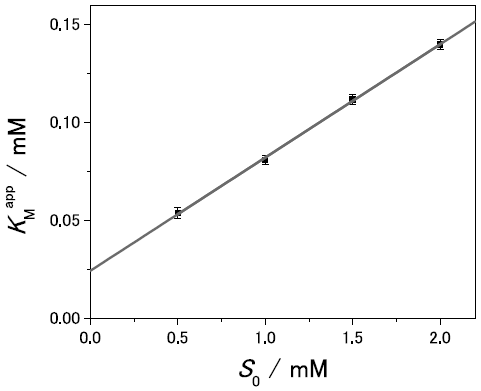
のように変化することになる。ここでKIは阻害定数 (阻害剤と酵素との解離定数)、KM0は真のミカエリス定数 (基質初濃度がKIよりも十分に低い場合に観測されるミカエリス定数) である。今回の場合の酵素・基質系の例では図3に示すように線型の関係が得られ、KM0とKIは、それぞれ25µM、0.42 mMであることがわかる。一方、今回の加水分解産物であるセロテトラオースとセロビオースについて個別に酵素阻害を調べた所、1 mMの濃度でもほとんど阻害を示さないことから、観測された阻害定数は、産物ではなく、基質によるものであることが示された。KM0を加水分解反応に至る酵素・基質複合体の解離定数と見るとすれば、加水分解が進行しないような酵素・基質複合体が存在し、その解離定数はこれより約30倍大きい (結合が弱い) ことがわかる。例えば、セロヘキサオースの酵素に結合する際に、本来のサブサイトからずれた位置に結合した複合体構造が形成されている可能性が考えられる。

従来、糖加水分解酵素の触媒活性には、高分子基質を用いる場合が多く、基質阻害の効果を明確に評価しやすいオリゴ糖を基質にした測定は少数であった。基質阻害が起きている場合には、基質初濃度の依存性を考慮しないと、ミカエリス定数は過大評価されてしまうことになり注意が必要である。本研究で紹介した手法では、基質初濃度を変えて測定することで容易に基質阻害の有無を判別可能であり、今後様々な酵素でこのような効果の有無が検証されることが期待される。これによって、酵素と基質との多様な結合様式やその熱力学的な安定性が定量的に議論できるようになることが望まれる。
5.異性化反応の観測と加水分解反応機構の判別
図1の反応では、オリゴ糖の反転型エンドグルカナーゼによる加水分解を観測したが、新たに生成した還元末端はα型の立体異性体 (αアノマー) をとることになる。水中ではαとβの2種の立体異性が平衡に存在するため、αからβへの立体異性化反応 (平衡状態への緩和反応) が進行することになる。この異性化はOH-イオンにより触媒されるため、酸性では非常に遅くてもpHが上がるにつれて反応速度は高くなると考えられる。
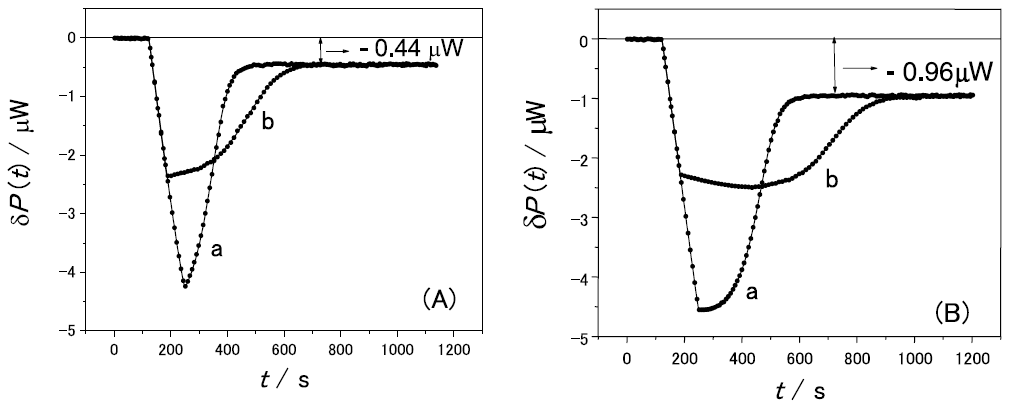
実際、pH7.0で図1 と同じ基質・酵素で測定したものを図4に示す。図1と同様に酵素の滴下に伴いグリコシド結合の加水分解の発熱が観測されるが、加水分解反応が終わった後でも、δP(t) は0に戻らず、ほぼ一定の発熱 (図4Aでは-0.44µW、Bでは-0.96µW) が観測される。この反応は基質初濃度の増加に伴って増加するが、酵素の濃度には無関係であることがこれらの図からわかる。反応速度が基質初濃度にほぼ比例していることから、加水分解の結果生じた還元末端の非酵素的な異性化反応であることが強く示唆される。

異性化反応の初期段階では、反応速度は加水分解反応の産物の濃度に比例すると近似できる。この時、この反応熱は3節の諸量とを使って
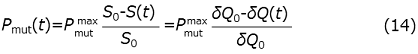
と近似される。ここで、Pmutmaxは異性化していない産物が基質初濃度と同じ濃度存在するときに生じる単位時間当たりの異性化反応熱である。
実際に、酵素による加水分解の吸熱速度 (式 (12) ) と、非酵素的変旋光反応の吸熱速度 (式 (14) ) の和を用いて観測値をfittingしたのが図4の実線である。全時間領域で観測値と一致していることがわかる。特に図4Bのbなどでは酵素溶液の滴下が終了した後に、さらに発熱速度が大きくなっている。通常の酵素反応の定常状態では説明できない現象だが、産物の濃度が高くなって異性化反応速度が大きくなったことでこのような現象が起こっていることがわかる。
このように時間経過を追うことで、同じ発熱反応を示す加水分解反応と異性化反応を分解して定量することが可能となった。これによって、糖加水分解酵素の中性条件下での活性評価が可能となった。異性化反応のような非酵素的反応と酵素反応とを実験的に判別するのは比較的容易である。すなわち、酵素反応速度は酵素濃度に比例するが非酵素反応速度は酵素濃度に依存しない。図4のA、Bのような条件の実験を行うことで、両者は明確に判別できる。
加水分解により生じる産物がβアノマーである保持型エンドグルカナーゼを用いた加水分解反応を図5に示す。この酵素は、セロペンタオースをセロトリオースとセロビオースに分解することをHPLCで確認している。加水分解による発熱反応に加えて、βからαアノマーに異性化する吸熱反応が酵素濃度に依存せずに観測されていることがわかる。この場合も観測値は、異性化反応を考慮した理論値で非常によく説明できることがわかった。

図4と図5でわかるように、中性pHで糖加水分解酵素活性を測定することで異性化反応を測定し、糖加水分解酵素の触媒機構を判別することが可能である。糖加水分解反応では、保持型酵素は一般塩基が基質を直接求核攻撃し、反転型酵素は一般塩基によって活性化された水分子が基質を求核攻撃することで触媒反応が進行すると考えられる。未知の糖加水分解反応がどちらの反応機構を持つかを実験的に判別するためには、産物のアノマーを同定する必要があるが、生じるアノマーによって異性化反応熱が必ず逆になることを利用すれば、他の糖加水分解反応にも今後容易に応用が可能と期待できる。
6.おわりに
最近の高精度熱量計を用いることで、酵素反応の際に生じる微小な発熱/吸熱をとらえ、酵素反応速度およびその時間変化を直接観測することが可能となっている。熱量測定というと生化学的な手法に比べて試料量が大量に必要であったり、感度が低いなどの印象があるかもしれないが、基質や酵素の濃度や使用量は通常の生化学的な方法とほとんど同様であり、しかも一度測定するだけで酵素活性のパラメーターを決定することが可能である。多くの分光学的測定で行われているように基質に観測のためのプローブを導入する必要もなく、観測したい酵素反応をそのまま測定できる。もしも感度が足りない場合には、別の化学反応をカップルさせることで感度を高めることも可能である。我々は、これまで蛋白質分解酵素や糖加水分解酵素で酵素活性の精密評価に本手法が有効であることを示してきたが、今後、更に様々な酵素にこの方法を応用し、その有効性を確かめてゆきたいと考えている。
これまで、糖加水分解酵素では、産物の示す副反応熱が大きくなる中性領域では、加水分解反応を熱測定で評価するのは難しいと考えられていたが、総熱量ではなく、吸熱速度の時間変化の測定によって両者を分離してとらえることが可能である。さらに、副反応の熱が観測されることを逆手にとって、酵素の触媒機構の判別が容易に可能なことを示すことに成功した。
現在使用されている生体分子用の高精度熱量測定は時間が表にでてこない静的測定がほとんどであるが、本稿で紹介したような動的な測定・解析を行うことで、今後、生体分子の構造形成や分子機能評価に更に応用分野が広がってゆくことを期待したい。
文献
1) 城所俊一: 蛋白質核酸酵素, 49, 1720 (2004).
2) 城所俊一他: 第5版実験化学講座第6巻, 日本化学会編, 丸善, 284 (2005).
3) Karim, N., Kidokoro, S.: Netsu Sokutei, 33, 27 (2006).
4) Karim, N., Okada, F., Kidokoro, S.: Thermochim. Acta, 431, 9 (2005).
5) Kidokoro, S.: Netsu Sokutei, 28, 74 (2001).
6) Karim, N., Kidokoro, S.: Thermochim. Acta, 412, 91 (2004).